1. Questions
Our question is, how do concentration predictions from six annual-average ambient PM2.5 empirical models for the contiguous US compare with each other? We investigate this question at three spatial scales: nationally, regionally, and urban/rural. Our two hypotheses are that model predictions will be (1) relatively similar to each other, because the models all use (as the dependent variable) publicly-available data from regulatory monitoring stations, or (2) relatively dissimilar because models differ in their methods and independent variables.
2. Methods
2.1. Input data
We obtained year-2010 predicted fine particulate matter (PM2.5) concentrations for six empirical models (see Table 1) via data download or direct request from researchers. Three models are “point based” (concentrations predicted at specific spatial locations):
-
CACES EPA-ACE: universal kriging with partial least squares data-reduction (PLS-UK) (Kim et al. 2020).
-
EPA downscaler: Bayesian space-time “fuse” of monitoring data and 12 km CMAQ model outputs (US EPA 2022).
-
MESA-Air models: space-time PLS with expectation-maximization to fill in missing observations (Keller et al. 2015).
The other three models are “gridded” (predictions are the spatial average within a grid-cell [e.g., a ~ 1 km2 area]):
-
Harvard/MIT EPA-ACE: generalized additive model, integrating multiple machine-learning algorithms (Di et al. 2019a).
-
SEARCH EPA-ACE: fusion of WRF-Chem, satellite data (MAIAC AOD), and a kriging of EPA monitor data (Goldberg et al. 2019).
-
van Donkelaar et al. (2019): statistically “fuses” a chemical transport model (GEOS-Chem), satellite observations of aerosol optical depth, and ground-based observations using a geographically weighted regression.
2.2. Processing of input data
We aligned spatiotemporal aspects of the models to be annual-average, by Census Tract (n ~ 74,000). For sub-annual (e.g., monthly) predictions, we calculated annual averages; for sub-tract predictions, we calculated Tract means; for gridded predictions, we converted to Census geographies by extracting values at block locations and then population weighting to the tract level.
One of the models (SEARCH model) is only available for the eastern half of the contiguous US (90° W longitude), which includes US cities as far west as Chicago. The other five models are available for the contiguous US.
2.3. Analysis
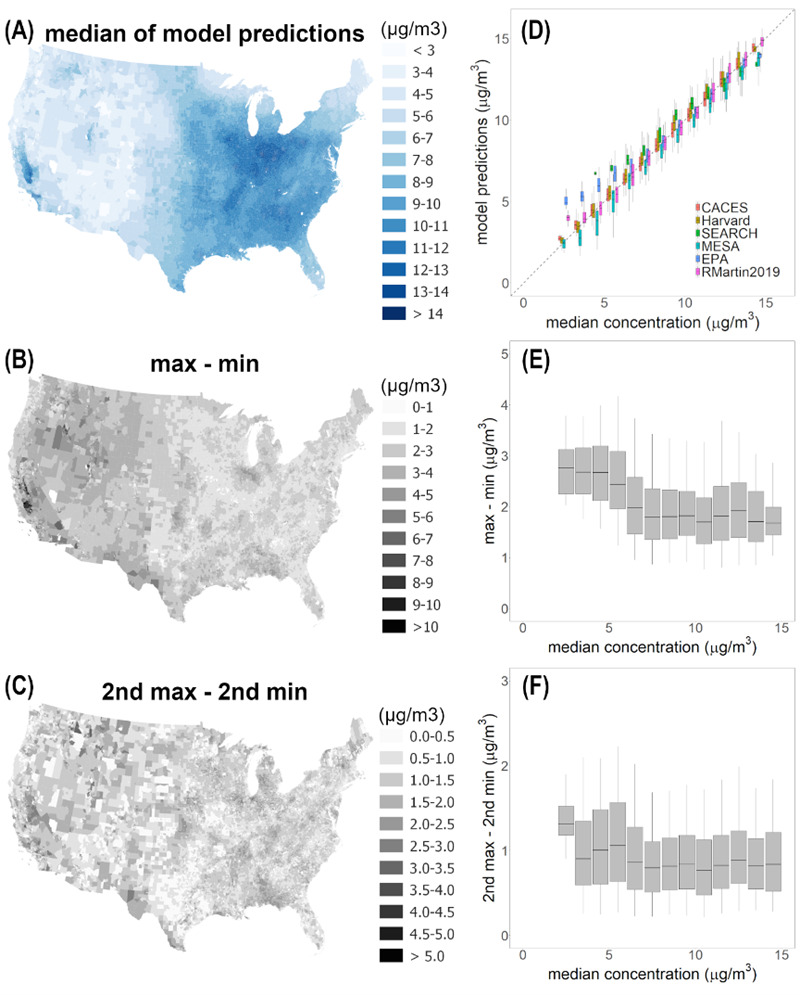
We conducted three pairwise comparisons of the model-predictions: (1) scatterplot matrices, (2) Pearson’s r, and (3) root mean square difference (RMSD) between predictions. We also generated boxplots showing distribution of predictions, and calculated the two values in each tract to indicate the range of model predictions: range (i.e., max minus min), and trimmed range (second-highest value minus second-lowest value).
We compare the individual model predictions against the median prediction of all models. The median measures central-tendency across models; absent further information, the median represents a “best estimate” or “ensemble forecast”. This study conducts model-model comparisons; it does not compare model predictions to monitoring or “gold-standard” data.
We conducted comparisons for (1) all locations, (2) urban vs. rural (urban defined as all tracts intersecting with Census urbanized areas, all remaining tracts are considered rural), (3) by region (using the 9 NOAA climate regions), and (4) stratified by population density (using the 2010 tract-level population density).
3. Findings
Predicted year-2010 PM2.5 concentrations range from ~2 to ~15 μg/m3. Pairwise scatterplots of model predictions (Figure 1) indicate a relatively high degree of agreement. The average Pearson correlation coefficient ("r") is 0.87 (range: 0.84 to 0.92), RMSD (units: μg/m3) is 1.1 on average (range: 0.8 to 1.4), and many best-fit lines are near the 1:1 line. The population average concentration of PM2.5 in 2010 was ~9.3 μg/m3 (mean), ~9.5 μg/m3 (median), so the RMSD (1.1 μg/m3) represents ~12% of the average concentration. Thus, nationally, the models agree well, supporting hypothesis #1, not #2.
When comparing the models separately by geographic region (Figure 2), we see modest differences among models for most regions, and minor differences between urban/rural locations. Based on r, model-model agreement is slightly lower in the Midwest and South than in other regions. RMSDs indicate agreement is slightly lower in the West.
The amount of variability among predictions, when displayed separately by concentration and location (Figure 3) indicates relative agreement among the models, across the range of concentrations (Figure 3D). In locations for which the median predicted concentration is comparatively low (less than 6 μg/m3), EPA predictions tend to be slightly higher than the other models. For the very lowest-concentration locations (median predicted concentrations less than 3 μg/m3), the Martin2019 predictions too tend to be slightly larger than the other models. The SEARCH model is only available for the eastern half of the contiguous US and so therefore excludes lower-population-density, lower-concentration regions found in the western half of the contiguous US. The CACES and Harvard models tend to agree with each other and to be near the median prediction, for each concentration range (Figure 3D).
The range of model predictions (a measure of between-model disagreement) is approximately constant (in units of concentration rather than in, e.g., percent-difference; see Figure 3E, 3F) across levels of pollution, suggests additive rather than multiplicative errors. To the extent that there is a pattern (more so for Figure 3E than Figure 3F), the range of predictions is greater in lower- than in higher-concentration locations. The finding reflects the patterns mentioned in the previous paragraph: below 5 or 6 μg/m3, the EPA predictions (and, below 3 μg/m3, the Martin2019 predictions too) are larger than the other models’ predictions; it suggests that predicting concentrations in low-concentration locations might be more challenging (greater model-model difference) than in medium- or high-concentration locations.
Overall, our findings are generally consistent with hypothesis #1, not #2. Model-model comparisons can identify the level of model agreement/disagreement, but not of accuracy or error. In cases where the models agree (or disagree), it’s possible all of the models are incorrect. A useful step for future research would be to compare against held-out measurements — either via a coordinated effort by the researchers to hold out a consistent set of measurements, or via an independent dataset of concentrations that none of the researchers employed in model-building.
Text in the Supplemental Information (SI) provides background on this research, describes strengths and weaknesses, and documents that results here are relatively robust to several sensitivity analyses.
Acknowledgements
We gratefully acknowledge the funders. This publication was developed as part of the Center for Air, Climate, and Energy Solutions (CACES), which was supported under Assistance Agreement No. R835873 awarded by the U.S. Environmental Protection Agency (EPA) for an Air, Climate, and Energy (ACE) center. Additional funding was from the EPA for the SEARCH ACE Center (RD83587101) and the Harvard-MIT ACE center (RD83479801). This manuscript has not been formally reviewed by EPA. The views expressed here are solely those of authors and do not necessarily reflect those of the Agency. EPA does not endorse any products or commercial services mentioned in this publication.



_and_root_mean_square_difference.png)


_and_root_mean_square_difference.png)