Evaluating the Vulnerability of the Sydney Train Network by Comparing Access-based and Network Centrality Metrics

1. Questions

Operational incidents are one of the significant threats to the smooth running of railway systems. Derailments, vehicle faults, power breakdowns, signal and shunting failures, intentional shutdowns, and emergencies disrupt the operation of the network temporarily or permanently. These incidents delay services both on and off-the affected route and consequently delay many passengers. These direct and side-effects are more consequential when the system is operating at its capacity (during peak hours) and vulnerable to disruption due to operational loads. Hence, the vulnerability of the rail transit network is a concern of managers and operators, and identifying critical stations, links, or regions under major incidents is crucial.

There is extensive research assessing network vulnerability and resilience using graph theory concepts, which abstract the physical structure of the network into links and nodes. Many of them study the vulnerability and resilience of road networks (Bell et al. 2008; Berdica 2002; Jenelius, Petersen, and Mattsson 2006; Yang and Qian 2012; El-Rashidy and Grant-Muller 2014; Scott et al. 2006) and some assess the reduction of network access before and after a system failure (Cui and Levinson 2017; Chen et al. 2006; Taylor, Sekhar, and D’Este 2006; Taylor and D’Este 2007). Some research investigates the vulnerability of public transport networks (Nassir et al. 2016; Rodríguez-Núñez and García-Palomares 2014; Cats and Jenelius 2012, 2014; Jiang, Lu, and Peng 2018) and measures the lost access by transit.

To date, graph-theoretic centrality measures have not been compared with access-based analysis. However, there are overlaps and inherent similarities in the aims and objectives of applying these methods. Different metrics provide different types of information. For example, closeness, betweenness and eigenvector centrality measures and provide ‘global’ information on the network structure by considering the entire network when ranking a single node. On the other hand, other network indices, such as the degree centrality measure, provide ‘local’ information on the graph structure by considering a single node and its neighbors. Access-based methods take into consideration a whole host of information on dynamic as well as static network structure, still in a ‘local’ way, but taking into consideration not only network structure, but travel times, origin-destination properties, and other land use factors.

Specifically, no comparison has been made between the reduction of access, when a station collapses, and the corresponding change in station rank in graph-theoretic and access-based analyses. To bridge this gap, this paper first defines disruption in the network and secondly, compares these methods. This paper also considers both the network structure and operational services to identify the critical links and nodes using spectral graph theory and compares the importance of critical nodes with their system-wide population-weighted access loss when an incident occurs.

2. Methods

2.1. Defining service-based network, and network failure

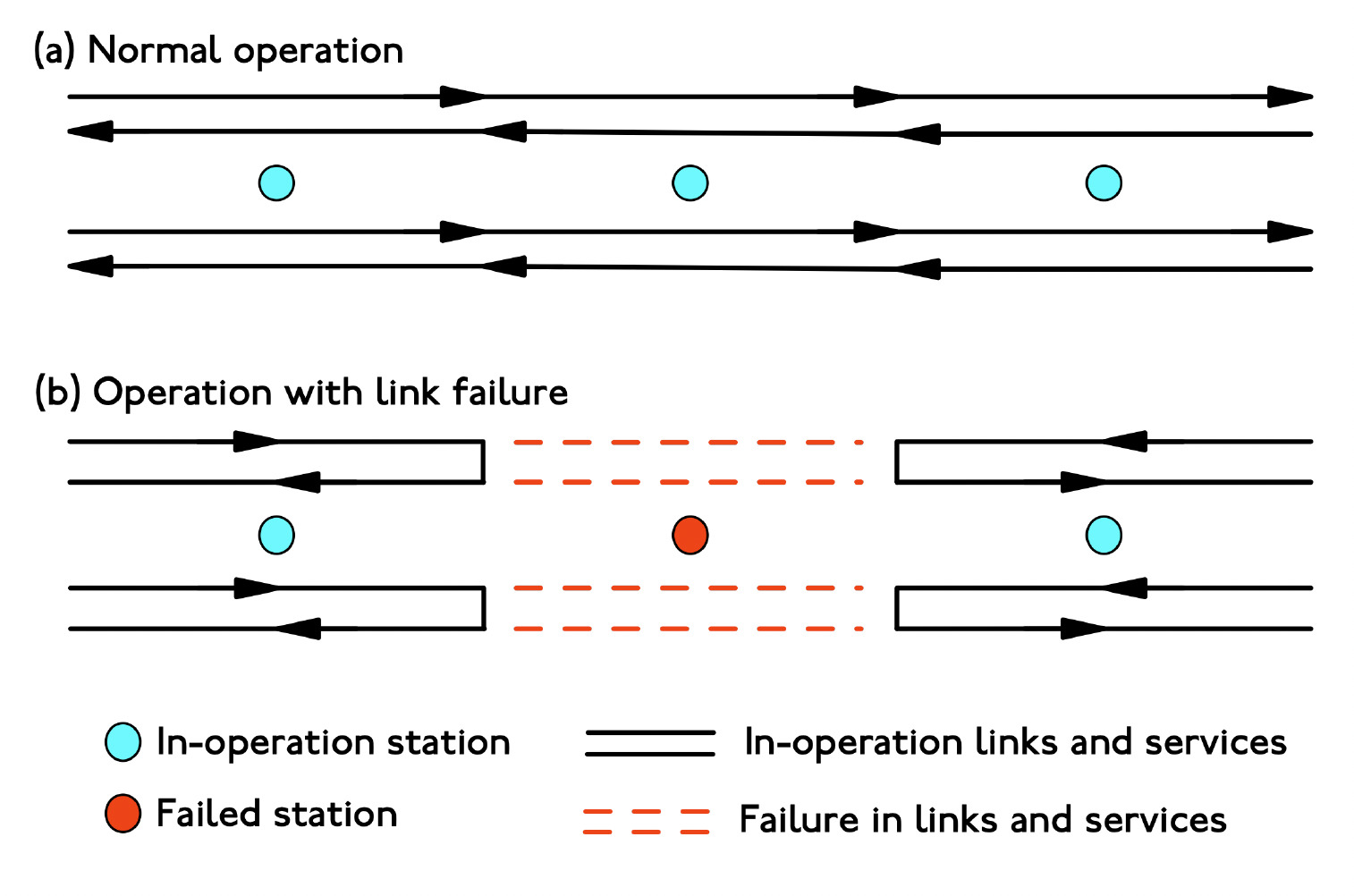
The railway network is a complex structure with different components including tracks, crossovers, and signals, and running services adds more dynamic complexity to finding the critical locations in the system. For example, regular and express services using the same set of tracks makes some of the stations more important than just taking the physical structure into account. To overcome that, this study uses service-based networks to define an abstracted graph (nodes and links). A service-based network has information about both the physical connections between stations and the scheduled services. Figure 1 illustrates the difference between structure-based networks and service-based networks.

Figure 1.The difference between structure-based and service-based rail network.

In a railway network, in general, failure can happen on stations and platforms (nodes) and along the connected tracks (links). To generalize the potential failures, we assume that a station failure means a node failure, and translates to discontinuity in the services (i.e., no through services) and that no trains can load/unload passengers at that station. In the access analysis, this has a significant impact on travel time between stations and thus between origins and destinations. However, the rest of the network can still operate and affected services can adjust to the new circumstances. For example, trains may be re-routed in some cases, changing the structure of the service network. This strategy can reduce the effect of cascading failures and mitigate access loss. Figure 2 displays an example of normal operation and adjusted operation before and after a failure in the network.

Figure 2.Comparison between normal and adjusted operation. In the access analysis, the person-weighted access for the adjusted operation will be compared against the normal operation.

In the adjusted operation, it is assumed that there are crossovers preceding and following the failed stations. Consequently, vehicles from upstream and downstream can return to their original terminal without completing their scheduled trips. In this study, a 3-minute delay is considered for shunting the vehicle into the opposite track route and initiating service in the opposite direction (1 minute for going forward, 1 minute for switching, and 1 minute for vehicle return). This strategy will be implemented to establish new services for measuring travel time in the access calculation.

2.2. Measures

This study uses four methods to evaluate and compare the critical nodes in a transit network:

• (I) service characteristics: the ratio of arrivals per number of platforms;

• (II) classic graph theory: traditional centrality measures of a planar graph to identify critical nodes;

• (III) considering spectral information: eigenvector centrality, that works with the leading eigenvector associated with the largest eigenvalue of the network’s adjacency matrix,

• (IV) access: the person-weighted access measure to rank the stations based on their access loss during a disruption.

The Supplemental Information explains these methodologies. These measures are calculated for the Sydney train and metro network provided in the standard GTFS. Extracting arrival information from GTFS files is discussed in (Chin et al. 2022).

3. Findings

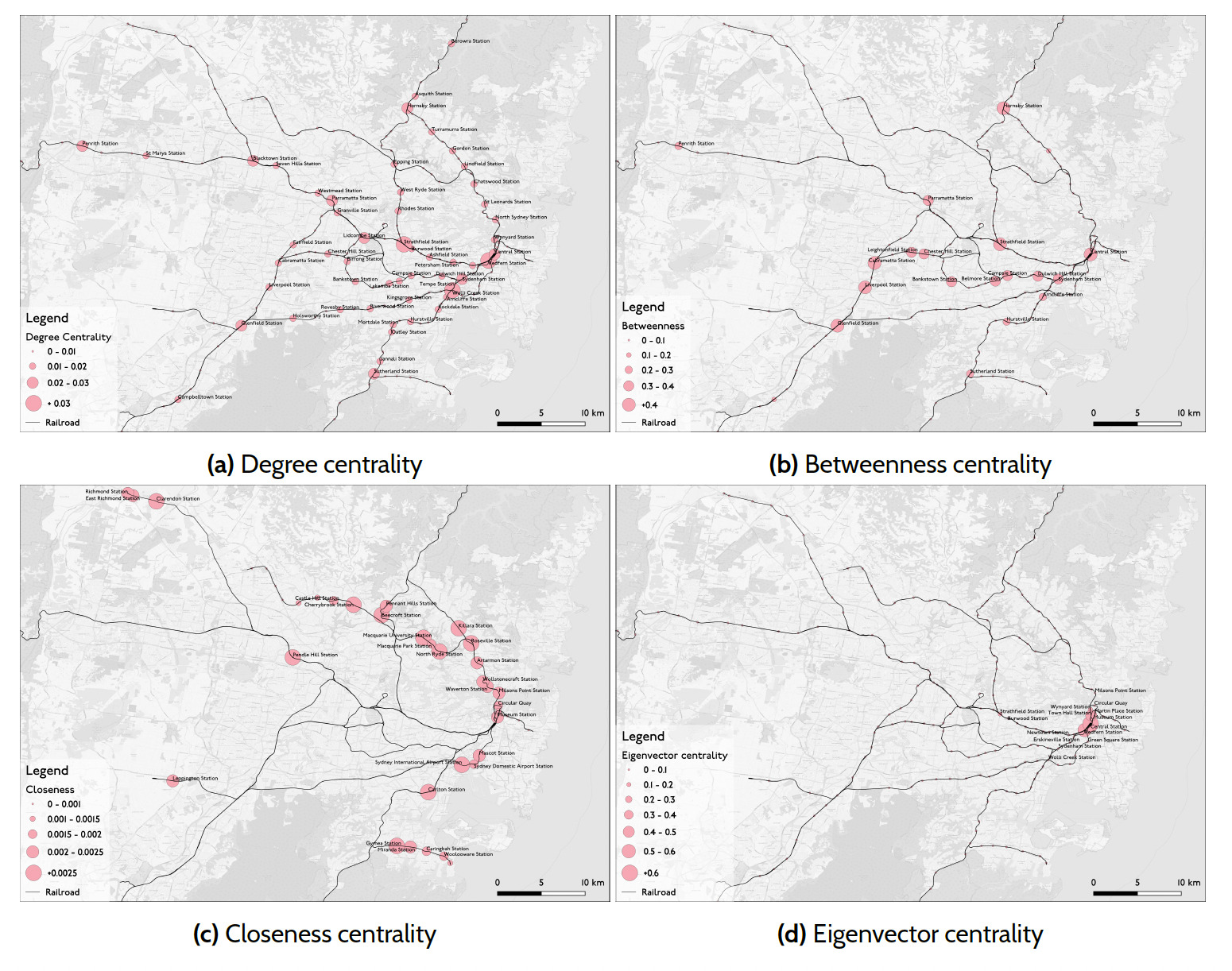
For calculating the graph centrality measures, the Sydney train network has been transformed into a weighted graph. The weights represents the number of services (i.e. count of passing trains) between each node pair. Then, the importance (rank) and centrality measures are calculated for each station on the network. Figure 3 demonstrates the four centrality indexes of each station, including degree, betweenness, closeness, and eigenvector centrality. The relative measures are illustrated using circles of different sizes. The analysis shows the stations in the city regions and inner west have high degrees of centrality, while stations with less centrality are farther out. The closeness centrality is higher for stations between transfers, and on the other hand, transfer stations have a higher betweenness than stations serving single lines.

Figure 3.Centrality measures of Sydney train network. The network is weighted by the number of arrivals (services) at each station.

Eigenvector centrality is highest for those stations which themselves are high centrality in the system, and are also connected to other high centrality stations. A very interesting finding is that when we consider the spectral information on not only each individual’s station’s centrality, but also the centrality of those other stations to which each station is connected, then eigenvector centrality only shows the central downtown hub-stations as central, and discounts all of the other stations in the network. This shows that the hub-and-spoke radial Sydney train network is highly dependent on this core hub, and any disruptions to this core makes the entire network vulnerable to failure. Another observation is that the resilience in the system is low, since if this central core hub fails, while the outer periphery of the network is unharmed, the alternative Sydney Trains pathways have very high circuity (Huang and Levinson 2015), and much slower transport modes (train replacement buses) would be required as a substitute.

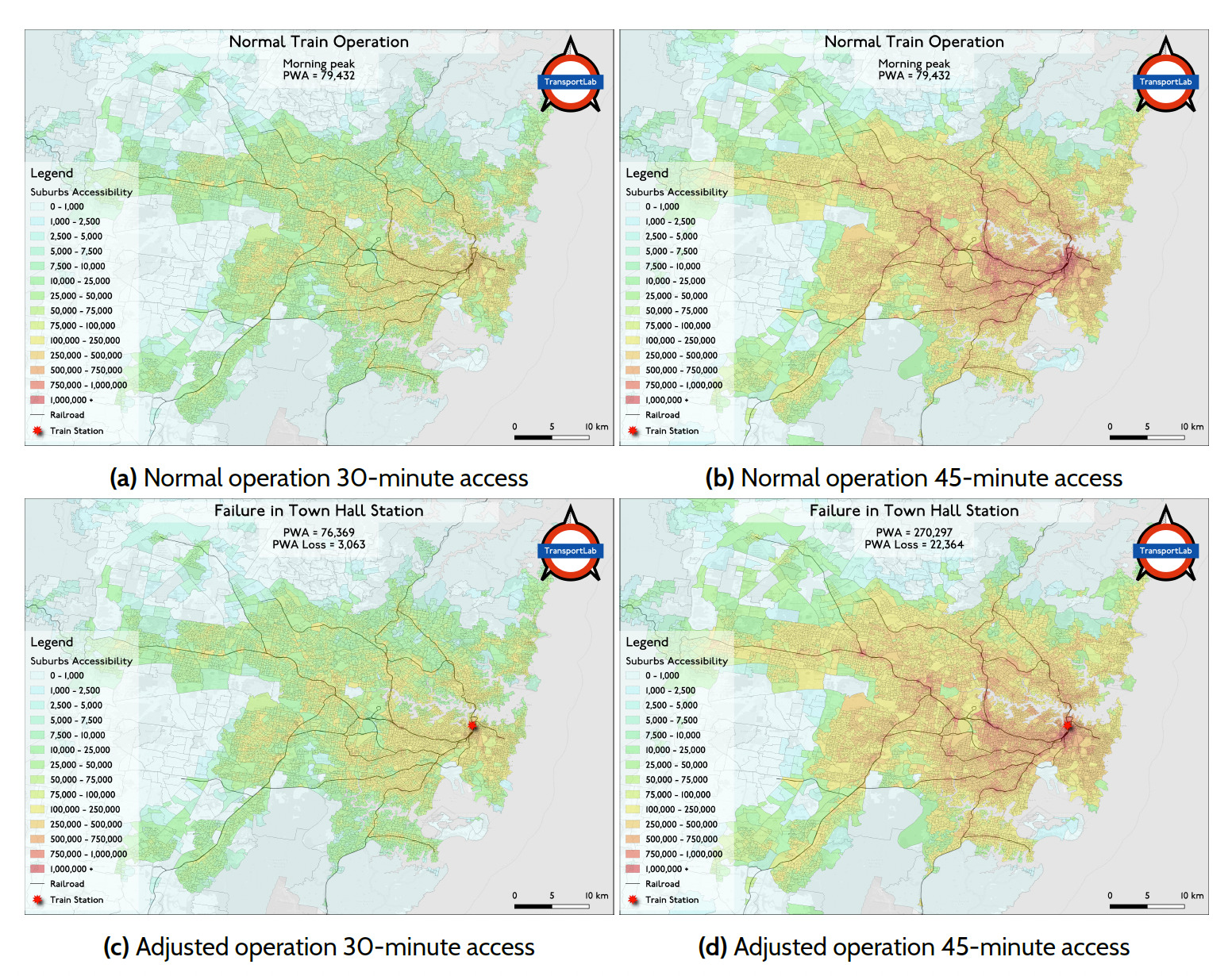
The access analysis considers the normal operation and failure of each node (before and after an incident). The assumption is that the network will adjust the trips in the upstream and downstream of the failure location as outlined in Figure 2. The stations are ranked by the person-weighted access loss (both 30- and 45-minute), and results indicate that Town Hall, Wynyard, Museum, Circular Quay, St James, and Strathfield Stations are the most vulnerable stations. It is worth noting that, except for Strathfield, all of these stations are located in the CBD. Figure 4 depicts the transit access for two time thresholds during normal operation (before the incident) and failure (after the incident) at Town Hall station.

Figure 4.30- and 45-minute access by transit; normal operation and failure in Town Hall Station. The person-weighted access represents the multi-modal performance.

Table 1 ranks Sydney train stations based on seven proposed measures, namely service ratio, degree centrality, betweenness centrality, closeness centrality, eigenvector centrality, 30-min person weighted access loss, and 45-min person weighted access loss. The ranking in the last column is based on the average score of all methods. The rankings vary significantly based on the employed metric. For instance, St James ranks first in terms of service ratio, whereas Strathfield ranks first in terms of average score. Strathfield, Redfern, and Central are, based on the average score, the top three stations. These stations have high rankings across most measures, indicating their importance in the transport network. However, from the access perspective, Central station is not considered a critical station due to the lower number of opportunities compared to other stations in the CBD and the presence of alternative bus routes in the vicinity. Degree centrality and betweenness centrality measures provide similar rankings, with Central and Strathfield consistently ranking high. In contrast, closeness centrality provides a different ranking, with predominantly outer stations such as Glenfield and Liverpool ranking high. Interestingly, eigenvector and access measure mostly rank the core (inner) stations within network as the most critical nodes. However, the 30-minute PWA loss and 45-minute PWA loss measures provide information on the system-wide impact of a station’s closure on the train network, taking into account other modes of transport and the existing land use pattern.

Results from the evaluations highlight the importance of considering multiple measures when analyzing and ranking transport networks, and perhaps combining alternative methods (Wu and Levinson 2021) if necessary to prioritize investments or repairs. It also highlights the importance of stations such as Central, Redfern, and Strathfield, which consistently rank high across most measures, indicating their crucial role in the Sydney transport network. Different measures provide different insights into the network’s structure and resilience, and a comprehensive analysis requires considering multiple measures simultaneously.

The availability of data and resources play a significant role in assessing network resilience. Graph-theoretic metrics demand less data, while access-based rankings require more data and involve computationally expensive processes. In this study, the physical structure of the network and track connectivity are inferred from formal services (GTFS), with an assumption of crossovers between stations. However, a more detailed network structure and precise locations of crossovers would yield more accurate results and offer comprehensive insights to transport planners and relevant transit agencies.

4. Supplemental information

4.1. Notation

Variables, parameters, and coefficients that will appear throughout this article are notated in Table 2.

4.2. Trip ratio index

The ratio of arrivals to the number of platforms at a station is one of the most straightforward ways to identify the most vulnerable stations in a network. The ratio illustrates the average load on each platform (i.e., how busy a station’s platforms are) and how a disruption in one track of rails (each track serves a platform) could affect station arrivals. The greater the ratio, the greater the station’s susceptibility to network failure and diverging trips. Equation 1 formulates the trip ratio index.

$$\alpha_i = \frac{A_{r,i}}{P_{l,i}}\tag{1}$$

where $\alpha_i$ is the trip ratio of station $i$; $A_{r,i}$ is the number of daily arrivals into station $i$; and $P_{l,i}$ is the number of operational platforms in station $i$.

4.3. Classic graph theory

The service-based network is converted to an undirected graph representation $G(V, E, W)$. The undirected graph demonstrates a bi-directional connection between each pair of nodes which compromises both single track with bi-directional services and double track with one-direction services. In the following, three graph-theoretic centrality measures used for evaluating the network vulnerability analysis are defined. It is important to note that the following measurements pertain to planar graphs (a planar graph contains edges that intersect only at their endpoints).

4.3.1. Degree Centrality

The degree centrality of a station represents the number of connections with other stations, and thus illustrates the connectivity and the importance of a station in the network. The higher the degree, the more central the station is (Golbeck 2013; Scheurer and Porta 2006). Degree centrality (normalized by dividing by the maximum possible degree) can be formally defined as Equation 2.

$$d_i = \frac{\text{Deg}(v_i)}{|V|-1} \quad \forall i \in V\tag{2}$$

4.3.2. Betweenness Centrality

Betweenness centrality measures how important a station is to the shortest paths through the rail network. It is the fraction of length (or number of links) of those shortest paths that include station $i$ and all the other paths (Cats 2017). The higher the betweenness, the more important a station is in traveling on the network. The betweenness centrality is written as Equation 3.

$$b_i = \sum_{j \ne k \in V } \frac{n_{j,k}(i)}{n_{i,j}} \quad \forall i \in V\tag{3}$$

4.3.3. Closeness Centrality

Closeness centrality of a station is the average length of the shortest path between the station and all other stations in the graph. Thus the more central a station is, the closer it is to all other nodes (stations). The shortest path length can be measured in number of links or unit of distance. Equation 4 shows the formal definition of closeness centrality.

$$c_i = \sum_{i \ne j \in V } \frac{1}{n_{i,j}} \quad \forall i \in V\tag{4}$$

4.4. Spectral graph theory

A transit network with the geographic structure and operational services can be demonstrated as a graph with weight attributes (there may be some levels of abstraction). Thus, the system is a weighted network $G = (V,E,W)$ where $V$ is set of nodes (transit stations), $E$ is set of links, and $W$ the associated weight values such as distance or the number of arrivals.

The adjacency matrix for network $G$ can be described as $A'_G = (a_{uv})_{N\times N}$ where $N = |V|$. The elements of the adjacency matrix ($A'_G$) are:

$$a_{uv} = \begin{cases} w_e & \text{if} \; e=(u,v) \in E\\ 0 & \text{otherwise} \end{cases}$$

where $w_e \in W$, nodes $u,v \in V$ and link $e=(u,v) \in E$.

The eigenvalues and the associated eigenvectors (spectra) of the adjacency matrix can be formulated as Equation 5.

$$A' \varphi = \lambda \varphi\tag{5}$$

where, $\varphi$ is the eigenvector and $\lambda$ is their associated values. Eigenvectors are mutually orthogonal and unit vectors.

4.4.1. Eigenvector centrality

Eigenvector centrality indicates that a station’s (node’s) importance depends on both the degree and importance of its neighboring stations. PageRank and HITS are eigenvector centrality measure derivatives. The relative centrality score of node $i$ can be defined as Equation 6.

$$x_i = \frac{1}{\lambda'} {\sum_{j=1}^{N}a_{ij} x_{j'}}\tag{6}$$

Where $\lambda'$ is a constant, and $x_{j'}$ is the centrality of neighbors. The computation of eigenvector centrality is an iterative procedure until a stable value is reached.

4.5. Person-weighted access

Calculating the accessis a way to measure the number of opportunities reachable in a specific time threshold. A person-weighted access measure is the number of opportunities (i.e. population in this study) at destinations reachable to the population at each origin. This index allows comparing the system-wide access by transit (Levinson, Giacomin, and Badsey-Ellis 2016).

The cumulative opportunities of block $i$ is represented in Equation 7.

$$A_{i,T} = \sum_{j=1}^{J} P_j f(C_{ij})\tag{7}$$

where $P_j$ is the population of region $j$, $C_{ij}$ is the generalized travel cost from region $i$ to region $j$, and $f(C_{ij})$ is the impedance function which:

$$f(C_{ij}) = \begin{cases} 1 & \text{if} \; C_{ij} \le T\\ 0 & \text{otherwise} \end{cases}$$

Person-weighted access could be formulated as the Equation 8.

$$A_{pw,T} = \sum_{i=1}^{I} A_{i,T} P_i\tag{8}$$

where $A_i$ is the cumulative opportunities of block $i$ to every other blocks reachable in time $T$, and $P_i$ is the population within region $i$.

The advantage of using person-weighted access is considering not only the physical structure of the train network at a large scale but also the covered land use layer.