Resilience: A Pathway Towards High Service Reliability in Telecommunication Networks

1. Questions

In the era of digitalization, new services and applications, such as remote surgery and self-driving cars, bring an unprecedented demand for a massive connected and highly reliable telecommunication network. 5G and its successive generation are designed to meet these requirements and capitalize on the potential opportunities. Nowadays, an increasing trend of deploying 5G technologies can be observed globally. More and more users have started to use 5G services. However, the reputation of 5G has been in part undermined by the occurred failures and resulting service disruption or loss of demand while employing devices manufactured under the new regime. The reliability of modern telecommunication is often questioned. Could new concepts, such as network resilience help deliver the promised reliability? Is resilience an unrealistic illusion or a practical pathway toward high reliability in the modern telecommunication network? This paper summarizes the findings as we explore the answers to these questions.

2. Methods

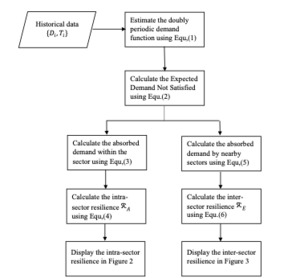
Network resiliency defines a network’s capacity to maintain adequate service levels by withstanding or recovering promptly to network disturbances (Hosseini, Barker, and Ramirez-Marquez 2016). The service performance of the ToC telecommunication hinges on the availability of base stations (Ohihoin et al. 2021). In the context of the paper, we investigate the service performance to mobile users in the area of interest after the failure of cells in the ToC telecommunication network to demonstrate the existence of resilience and its impact. A base station in the ToC telecommunication network is a hierarchical system that is composited of three sectors, and each sector contains multiple cells. In the practical ToC network, if all cells within a base station are functional, the demand is often satisfied. Thus, the demand could be observed and equivalent to the downstream traffic of the base station. Based on the data provided by Huawei, the hourly demand $D_{i}$ is recorded in the format $\left\{ D_{i},T_{i} \right\},$ here $T_{i}$ signifies the timing of the recorded demand. Due to the demand $D_{i}$ often manifests as a doubly periodic function (both daily and weekly). The methodology of our approach is illustrated in the flowchart, as shown in Figure 1.

Figure 1.Flow chart of the research methodology

Firstly, we apply the Fourier Series $s_{N}$ to capture the underlying dynamic of the demand.

$$D_{i}=s_{N}\left(T_{i}\right)+\varepsilon \tag{1}$$

where $\varepsilon$ indicates the residual. By analysing the practical data, the $\varepsilon$ is appeared to be normally distributed with 0 mean and variance $\sigma^{2}.$ If the cells malfunction or fail, then the downstream traffic will be reduced and may not be able to reflect the actual demand.

To quantify the loss of demand, we then utilize the Expected Demand Not Satisfied (EDNS) during the period of failure $\left(\tau_{1}, \tau_{2}\right)$ (Li and Jia 2021) as:

$$\begin{align} E D N S&=\mathbb{E}\left[\sum_{\forall \tau_{1} \leq T_{i} \leq \tau_{2}} \sup \left(0, s_{N, L}\left(T_{i}\right)-D_{i, L}\right)\right]\\ &=\sum_{\forall \tau_{1} \leq T_{i} \leq \tau_{2}} \mathbb{E}\left[\sup \left(0, s_{N, L}\left(T_{i}\right)-D_{i, L}\right)\right] \end{align} \tag{2}$$

where $D_{i,L}$ is the summation of observed downstream traffic of malfunctioned cells and $s_{N,L}$ indicates the approximated demand based on the historical data collected during the cells are functional. The loss of demand could be absorbed by remaining functional cells in the sector. $A D_{A}\left(T_{i}\right)$ represents the absorbed demand at the time $T_{i}$. We use the subscribe L and A to indicate the cells with demand loss and demand absorption, respectively. $A D_{A}\left(T_{i}\right)$ can be expressed as:

$$A D{A}\left(T{i}\right)= \begin{cases} \begin{aligned} 0&, D_{i, A}-s_{N, A}\left(T_{i}\right) \leq 0 \\ D_{i, A}-s_{N, A}\left(T_{i}\right)&, 0 < D_{i, A}-s_{N, A}\left(T_{i}\right) \\&\quad < D_{i, L}-s_{N, L}\left(T_{i}\right) \\ D_{i, L}-s_{N, L}\left(T_{i}\right)&, D_{i, A}-s_{N, A}\left(T_{i}\right) \\ &\quad \geq D_{i, L}-s_{N, L}\left(T_{i}\right) \end{aligned} \end{cases} \tag{3}$$

where $D_{i,A}$ is the observed demand at the remaining functional cells, and $s_{N,A}$ represents the approximated demand based on the historical data collected during the cells are functional. We define this type of demand absorption by the cells within the same sector as intra-sector resilience. Even if one or more cells fail in the sector, as long as the remaining cells can support the demand, there will be no significant loss of demand. The intra-sector resilience can be expressed as:

$$\begin{align} \Re_{A}=\frac{1}{E D N S} \sum_{\forall \tau_{1} \leq T_{i} \leq \tau_{2}} A D_{A}\left(T_{i}\right) \end{align} \tag{4}$$

Absorption of demand upon cell failure may also exist beyond the sector level. Unlike the absorption within the sector, the absorption amongst different sectors is often spatially limited as the coverage between sectors is only partially overlapped. Let $j$ be the index for neighborhood sectors. The parameter $\gamma_{j}$ is introduced to reflect the partial absorption $0 \le \gamma_{j} < 1$ and $\sum_{\forall j} \gamma_{j} \leq 1$. Thereby, the absorption between sectors could be expressed as:

$$A D{E}^{[j]}\left(T{i}\right)= \begin{cases} \begin{aligned} 0&, D_{i, A}^{[j]}-s_{N, A}^{[j]}\left(T_{i}\right) \leq 0 \\ D_{i, A}^{[j]}-s_{N, A}^{[j]}\left(T_{i}\right)&, 0 < D_{i, A}^{[j]}-s_{N, A}^{[j]}\left(T_{i}\right) \\ &\quad < \gamma{j}\left(D_{i, L}-s_{N, L}\left(T_{i}\right)\right) \\ \gamma{j}\left(D_{i, L}-s_{N, L}\left(T_{i}\right)\right)&, D_{i, A}^{[j]}-s_{N, A}^{[j]}\left(T_{i}\right) \\ &\quad \geq \gamma{j}\left(D_{i, L}-s_{N, L}\left(T_{i}\right)\right) \end{aligned} \end{cases} \tag{5}$$

Here, the $A D_{E}^{[j]}$ denotes the absorption by exterior neighborhood sectors $j$. We refer to the demand absorption by nearby sectors as inter-sector resilience. Even if all cells within a sector are completely failed, the loss of demand within the shared regions of its neighborhood sectors could be partially compensated. The inter-resilience can be expressed as:

$$\Re_{E}=\frac{1}{E D N S} \sum_{\forall j \forall \tau_{1} \leq T_{i} \leq \tau_{2}} \sum_{E} A D_{E}^{[j]}\left(T_{i}\right) \tag{6}$$

Next, we explore the practical behaviors of both $\Re_{A}$ and $\Re_{E}$ in ToC telecommunication networks.

3. Findings

Based on the practically collected data, we focus on investigating the behavior of the malfunctioned base station and its neighborhoods. Case I represents a typical scenario in which cells with a sector are partially failed. In this case, both the loss of the demand and absorbed demand from the remaining functional cells can be visualized in Figure 1. To overcome the influence caused by $\varepsilon,$ the confidence region (95%) is also plotted.

From Figure 2, we can clearly observe an increase in demand traffic on the remaining functional cells. Evidently, both the loss of demand and absorbed demand are significant (exceeded the confidence region). The EDNS and the expected absorbed demand are 78.71GB and 13.67GB, respectively. Thereby, the calculated $\Re_{A}=13.67 G B / 78.71 G B=17.36 \%$.

Figure 2.A typical case for intra-sector resilience

In the case illustrated in Figure 3, the EDNS and the expected absorbed demand are 148.84GB and 12.79GB, respectively. $\Re_{E}=12.79 G B / 148.84 G B=8.59 \%$.

Figure 3.A typical case for inter-sector resilience

We found both intra-sector resilience and inter-sector resilience can compensate for the loss of demand upon partial or complete failure of cells within a sector. Thereby, it may be unnecessary to schedule a maintenance action immediately after a cell failure event. In the light of both intra-sector and inter-sector resilience, the maintenance schedule should be re-prioritized. In a practical ToC telecommunication network, resilience can preserve the serviceability and open up a successful way toward high reliable telecommunication.

Acknowledgment

We are grateful for the support from Huawei.