1. Questions
On-demand ride-sourcing service has reshaped transportation services via online orders and dispatching service vehicles (Shaheen and Chan 2016). In a duopoly market, passengers can make orders on both platforms, making order cancellation a prevalent and significant issue, which is not only unproductive but adds to congestion. Under travel time uncertainty, service arrivals become uncertain. Passengers may have different perceptions of the service arrival time, which impacts their order cancellation behavior in a stochastic manner and hence the optimal pricing strategy (Durrande-Moreau 1999). The strategy of cancellation penalty acts as critical leverage to manage the cancellation behavior (He et al. 2018; Li, Li, and Guo 2021; Wang et al. 2019). Using the monopoly market (MM) as a benchmark, this study investigates the duopoly market (DM) with competitive platforms from three perspectives: passengers, the platform(s), and society as a whole. The questions include: will the MM or the DM perform better under these three perspectives, and if so, for a fresh market or for a mature market?
2. Methods
In a DM with two ride-sourcing platforms A and B, we address two types of cancellations. The first type is random cancellation with a given probability due to customer trip changes, which happens to both the MM and the DM. The second type is stage-II cancellation arising from passengers ordering from two platforms and subsequently canceling one, which only happens in the DM, as depicted in Fig. 1. Based on the two types of cancellations, we develop a modelling framework, as described below.
Stage-II order cancellation: In stage-I, passengers choose to order ride-sourcing services from platform A only, from platform B only, or from both platforms A and B, or they take an alternative public transport mode. In stage-II, passengers ordering from both platforms must choose between (i) cancel the first-arrived vehicle and wait for the vehicle yet to arrive, or (ii) take the first-arrived vehicle and cancel the vehicle yet to arrive. The cancellation decision is made according to the cost-benefit analysis between (i) cancel the first-arrived vehicle, pay its penalty, and wait for and pay the vehicle yet to arrive; (ii) take and pay the first-arrived vehicle, and cancel the vehicle yet to arrive and pay its penalty. The analysis involves the tradeoff between the total price (fare and cancellation penalty combined) and the expected arrival time of the vehicle yet to arrive, as derived from the vehicle arrival process.
Waiting time perception: The probability of stage-II cancellation is significantly influenced by the waiting time perception of passengers. Under different traffic conditions, peak versus off-peak, passengers may perceive the vehicle arrival times differently. Note that the waiting time mainly refers to the pickup time here, and the matching time, which is short, often in seconds, is omitted. In the off-peak period, they perceive that the pickup times are less affected by congestion that introduces travel time variability. Hence, they are optimistic about vehicle arrival times and perceive that the vehicles will arrive earlier than what is expressed by the Poisson process. In contrast, during the peak period, passengers are pessimistic about vehicle arrival times and perceive that the vehicles will arrive later than the Poisson process. Thus, we model the perceived vehicle arrival rate as increasing (decreasing) under uncongested (congested) conditions.
Supply-demand equilibrium: For each platform, the vehicle arrival time is determined by demand and supply, which in turn influences passenger mode choice and order cancellation behavior, forming an endogenous equilibrium given fare and cancellation penalty of each platform. Note that ride-pooling is not considered in our model.
Nash equilibrium: A Nash equilibrium is reached when no platform can improve its revenue by unilaterally changing its fare or penalty. Similar to Zhang and Nie (2021), we formulate a variational inequality problem (VIP) to find the optimal fare and penalty of each platform.
By considering the components above, the pricing problem in the DM is formulated as a bi-level optimization problem. In the lower level, travelers choose the travel modes and the platform(s) to make orders according to the logit model, subject to the inhomogeneous Poisson arrival process; whereas the upper level is to determine the trip fares and cancellation penalties to achieve Nash equilibrium between the competing platforms. In this manner, the fare and penalty variables will influence the supply-demand equilibrium, yielding different profits for both platforms, which are optimized to achieve the Nash equilibrium. The optimal pricing strategy is obtained by solving the VIP using an iterative algorithm.
The formulation of the MM shares similarities with the DM in the supply and demand equilibrium. For the MM with only one platform, only random cancellations happen. The cancelation penalty, nevertheless, will influence passengers’ potential trip cost and thus the supply-demand equilibrium. Based on the fixed-point equilibrium, the platform will optimize the penalty and fare strategy to improve its revenue.
3. Findings
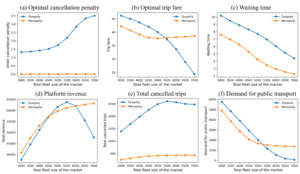
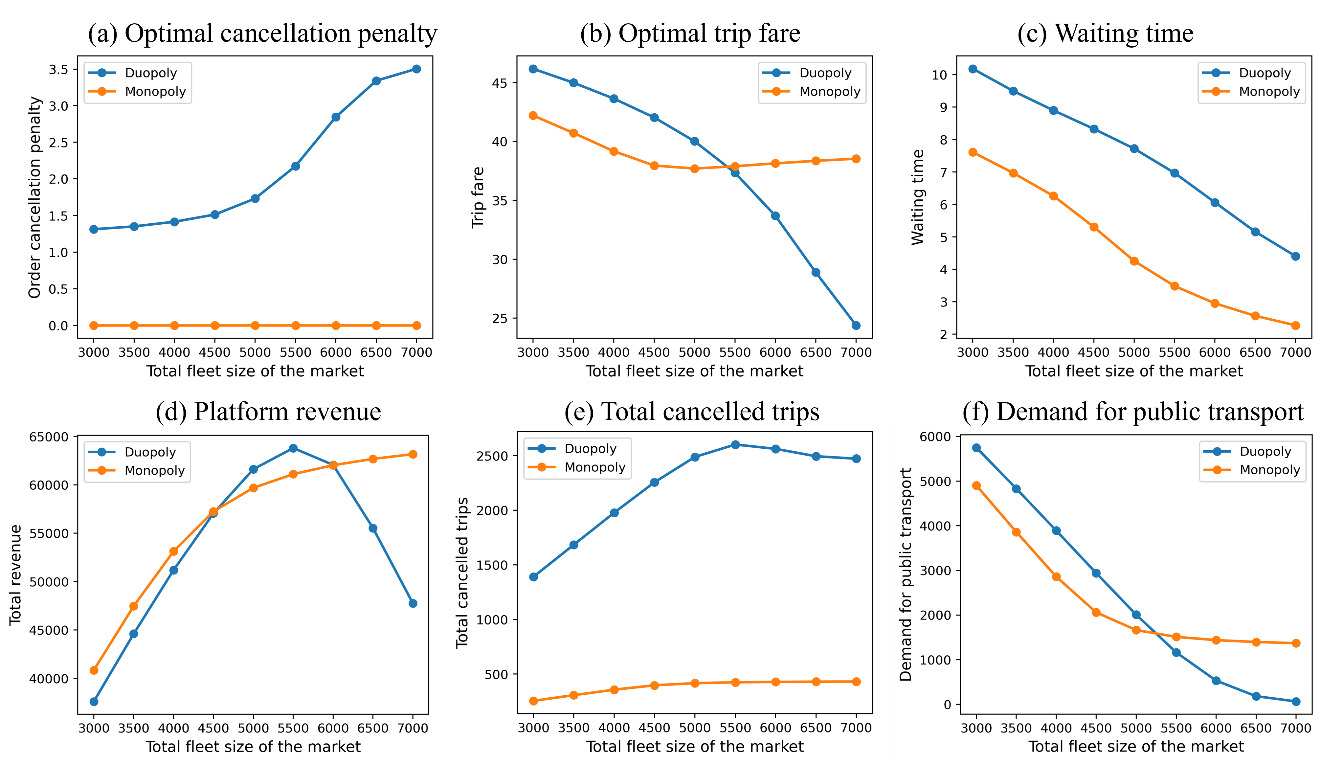
To compare the MM versus the DM, we set both markets to have the same total fleet size, with each platform in the DM having half the fleet size of the platform in the MM. Focusing on the congested period, we derive the cancellation probability based on the perceived decreasing arrival rate. By varying the total vehicle fleet size of the markets from 3000 to 7000, the results of market equilibrium are given in Fig. 2.
From passengers’ perspective, the results can be analyzed based on the cancellation penalty, fare and service waiting time. For the cancellation penalty, the results show that: (1) the MM sets a zero penalty while the DM sets a higher penalty; (2) with increases in the fleet size, the DM further increases their penalties to restrict order cancellation. As for the fare, the results show that: (1) with a larger fleet size, both the MM and DM lower their fares to attract more demand, while the DM lowers the fare even more; (2) the fare of the MM is lower (higher) than the DM when the total fleet size is smaller (larger) than the critical value, around 5500. This indicates that a merger of equals is good for passengers when the total fleet size is small. When the fleet size gets larger, the fare of the MM becomes more expensive than the DM.
From the platform’s perspective, the MM will enjoy a higher revenue both when the fleet size is small and when it is large, i.e., excluding the mid-range fleet sizes. In a new market, when the fleet size is small, the MM is the most preferred, and when the market becomes large, a merger of equals is also beneficial to the MM operator.
From society’s perspective, the total cancelled trips of the MM are always lower than those of the DM. As for public transport ridership, it decreases with the ride-sourcing fleet size. The demand for public transport is lower in the MM when the fleet size is small, and the trend is reversed when the fleet size is larger.
In summary, the MM is a good way to start, with low cancellation penalty, low fare, and short waiting time, compared with the DM. As the fleet size builds up, the MM is still better in terms of cancellation penalty and waiting time, but its fare will be higher than the DM. The platform also prefers the MM, both when the fleet size is small as in a new market or when the fleet size is large as in a mature market. As for total cancellations, the MM also performs better. One potential downside of the MM may be that its good performance will take away public transport demand in a new market. These results show that under waiting time uncertainty and order cancellation, the MM is a good choice for both passengers, the platform, and society as a whole, especially in a new market.
As for a mature market, with a large fleet size, the DM will offer a lower fare, but it will have lower performances in terms of service waiting time, revenue, and total cancellations. From a fresh market toward a mature market, i.e., in the mid-range fleet sizes, the DM will offer a higher revenue and therefore may be preferred by the platforms, despite having high total cancellations.
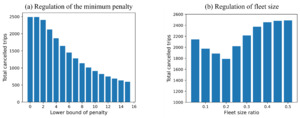
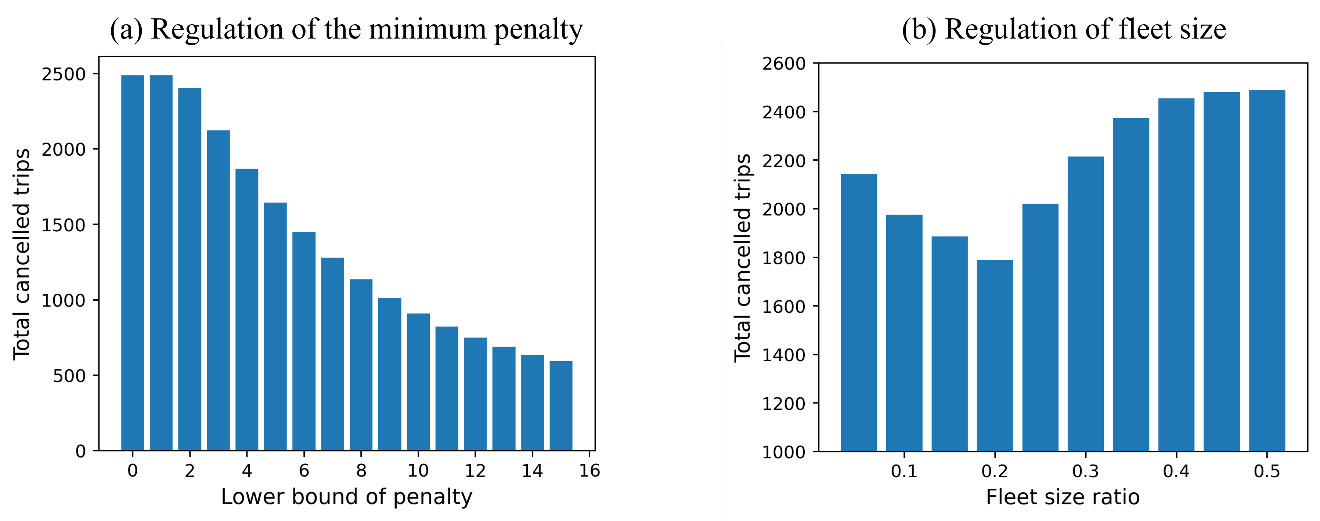
To guard against this wasteful behavior, regulatory measures in the DM can be introduced. Specifically, we study two possible measures: (I) minimum penalty and (II) fleet size ratio control. Fig. 3 shows the Nash equilibrium results under regulatory constraints while fixing other parameters. For the first measure, by setting a minimum cancellation penalty from 0 to 15, the number of total cancellations decreases from around 2500 to around 600. Setting a higher minimum penalty is effective in reducing cancellations. Nevertheless, it should not be too high, and should be determined considering the average fare. In the second measure, the fleet size ratio refers to one platform’s fleet size over the whole market fleet size. By varying the ratio from 0.1 to 0.5, the total cancellations first go down and then go up, obtaining a minimum at 0.2, which indicates that asymmetrical fleet sizes are preferred. Since different fleet size ratios lead to different cancellation results, potential regulations could be implemented.
Acknowledgments
Our work is supported by the General Research Fund #16212819 of the Research Grants Council of the HKSAR Government, and National Science Foundation of China (No. 71890970, No. 71890974). The author also gratefully acknowledges the financial support from the Hong Kong PhD Fellowship.