1. Questions

Street parking is a notoriously contentious issue. Limited street parking has been raised in opposition to diverse projects ranging from bike lanes to residential development (Arancibia et al. 2019; Taylor 2020). Furthermore, cruising for parking when demand exceeds street parking capacity has been shown to substantially contribute to traffic volumes and greenhouse gas emissions from driving (Shoup 2007; Millard-Ball, Weinberger, and Hampshire 2014). Commonly, stakeholders debate the preservation of street parking or the allocation of off-street parking, but some capacity can be created at no cost by increasing the efficiency of existing street parking. Here we quantify this benefit by investigating the steady-state conditions that arise when parkers follow various rules about where to place their car in the available space. We address the questions:

• What is the optimal strategy for parkers to align their vehicles in an available space in a parallel parking setting?

• How do the benefits of the strategies change as the context approaches the short or partial block-faces often available in urban settings?

2. Methods

The findings presented here are based on a simulation of vehicles arriving at an unbroken stretch of curbside parallel parking. In each simulation, the vehicles all follow the same rule about where to align within the available space. This rule can be one of the following:

One end — They park as far forward in the space as possible.

Either end — They park as far forward or backward as possible, with an equal probability of either.

Middle — They park in the middle of the available space.

Random — They align randomly within the available space.

The vehicle lengths are assumed to follow a normal distribution with a mean of $\mu = 5$ m and a standard deviation of $\sigma=\frac{2}{3}$ m (Kwon, Varaiya, and Skabardonis 2003; Coifman and Kim 2009; Peters, de Haan, and Scholz 2015). The values encompass both the variability in physical vehicle length as well as the distribution of gap acceptances that the drivers demonstrate when parallel parking. Initially, the site is vacant and vehicles arrive to occupy parking spaces following one of the above rules. If a vehicle arrives that cannot fit in any remaining space, a vehicle departs (unparks) leaving a new gap. There is a queue of vehicles waiting to park, and the first vehicle in that queue will wait until there is a gap that it can fill before the next vehicle can access any gap. The complete simulation algorithm is available in the Supplemental Material.

The simulation’s primary performance metric is linear density which is a measure of efficiency where 1 represents a site that is fully occupied by vehicles and 0 represents an empty stretch of road. Linear density is defined as the ratio of the total length of the vehicles parked at a block-face, including their gap acceptance, to the total length of the block-face itself, $L$. After initialisation, the simulation maintains a demand that exceeds capacity, so any value less than 1 should be interpreted as inefficient packing of vehicles rather than insufficient demand.

The simulation also records the distribution of vehicle lengths that were generated and the corresponding gap size distribution. The simulation code itself is available open source at https://github.com/benjym/parking.

3. Findings

The behaviour of the system as vehicles depart and are replaced along a 50m block-face is shown in Figure 1 for vehicles following each strategy. Vehicles are coloured randomly, and white space represents no vehicles. The packing density changes from bottom to top, which is indicated by a change in white space.

Figure 1.Spatiotemporal diagram for vehicles parking using the four identified strategies. Vehicles are coloured randomly, and white space represents no vehicles. The packing density decreases from bottom to top, which is indicated by increasing white space.

The reference case for packing efficiency is taken to be pre-marked parking locations with uniform lengths. In Figure 2, two benchmarks are shown for pre-marked parking spaces with length $l_1=\mu+2\sigma$ (dashed line) or $l_2=\mu+3\sigma$ (dotted line), which allow for 97.7% and 99.9% of vehicles to park, respectively, and vehicles too long to park are ignored.

Figure 2.Impact of vehicle alignment strategy on parking system for long block-faces ($L=10^4$ m). Each strategy is represented with a different colour. Left: Density of vehicle packing as a function of how many vehicles depart the block-face. Right: Gap size distribution at the final state after $10^4$ vehicles have departed.

These can be compared with paradigms where parking spaces are dynamically defined by the neighbouring vehicles. When parkers align their vehicles at the same end of any available space (One end strategy), the initial packing (left edge of Figure 2 Left), is close to 100% efficient for long block-faces, with only a small available space at one end. As vehicles depart and randomly-sized vehicles replace them, the packing approaches a steady state shown on the right edge of the same figure. In the One end strategy, it decreases in efficiency, but only to approximately 93%, as shown in Figure 2 Left. Similar behaviour is observed when parkers choose to park at either the front or back of any space with equal probability (Either end strategy). When parkers position randomly or park in the middle of a space, a lower linear density is observed for all times, i.e. the space is initially less dense and remains less dense as vehicles leave and are replaced. As can be seen in the gap size distribution in Figure 2 Right, less efficient packing corresponds to the occurrence of more gaps along the block-face, although fewer large gaps ($>3$ m). When compared to the baseline cases of pre-marked gaps with lengths $l_1$ and $l_2$, a linear density of 93% corresponds to an increase of 18% or 30% in the number of vehicles along the block-face, respectively.

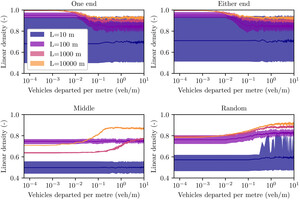
As the length of the block-face approaches the length of the vehicles, the boundary conditions become more important, as shown in Figure 3. Even for relatively short block-face lengths ($L=10$ m), there is a systematic improvement in packing efficiency for the One end and Either end strategies over the other two strategies. All the strategies are advantageous over marked spaces.

Figure 3.Packing efficiency as a function of block-face length $L$ for the four parking strategies. The solid lines represent the mean value, and the bounds of the coloured areas represent 20^th and 80^th percentiles from the simulation of a total of 10,000m of block-faces for each block-face length.

Parking is one of the most powerful policy levers for managing travel demand since both the cost and inconvenience of parking can deter travellers from driving. It is also a contentious issue for community advocacy with the wide deployment of residential parking programs making explicit the prioritisation of curbside parking for residents (Moylan, Schabas, and Deakin 2014). Moreover, the decreased requirements for parking are a frequent selling point of autonomous vehicle systems, with manufacturers and policy makers pointing to alternative uses of the space. We show that the four strategies identified here make systematic differences to the density of parked vehicles for a range of block-face lengths. The findings indicate that by instructing parkers, whether autonomous or human, to park at one end of any available gap, a significant increase in parking density can be achieved relative to other strategies for a range of block-face lengths and heterogeneous vehicle lengths. All strategies offer efficiency advantages compared to pre-marked spaces, and short block-faces (10m), often created by curb cuts for driveways, reduce efficiency and increase variability.

Acknowledgements

The authors would like to thank their anonymous neighbours whose erratic parking inspired this work.