The Revealed Preference for Battery Electric Vehicle Range

1. Questions

The primary drawback of battery electric vehicles (BEVs) as opposed to internal combustion engine (ICE) vehicles is their limited range. To enhance the competitiveness of BEVs, extended range might be useful. Exactly how do car buyers value battery electric range? How does the willingness-to-pay for extended range depend on the initial range?

2. Methods

The BIG-5.3 discrete choice model of automobile purchase is a disaggregate, generic nested logit model estimated on a data set including 2 184 804 individual new passenger car transactions between January 2003 and May 2019 in Norway. Without loss of information, we collapse the set of individual transactions into 40 301 rows (‘observations’), each describing a given model variant of which at least one specimen was sold in a given year. Weighting each observation by the number of identical model variants sold, we derive maximum likelihood estimates predicting the market share of each model variant in each year. For a more complete account of the model structure and estimation the reader is referred to Fridstrøm and Østli (2021a, 2021b).

In essence, the model distinguishes between five different energy technologies (market shares in 2020 in parentheses):

• Gasoline internal combustion engine (ICE) vehicles (6 percent)

• Diesel ICE vehicles (8 percent)

• Ordinary (non-plug-in) hybrid electric vehicles (HEVs) (11 percent)

• Plug-in hybrid electric vehicles (PHEVs) (20 percent)

• Battery electric vehicles (BEVs) (55 percent)

Many vehicle demand models, including ours, treat the retail prices as exogenous. However, as pointed out in the seminal paper by Berry, Levinsohn, and Pakes (1995), automobile prices could be endogenous on account of unobserved product characteristics. This could bias our price coefficient towards zero.

We believe, however, to have reduced the scope for endogeneity bias by using the manufacturer’s suggested retail prices, or ‘list’ prices, rather than the individual transaction prices negotiated between the individual customer and her car dealer, and by including a wide set of quality attributes among the explanatory factors, such as size, powertrain, ICE type approval fuel consumption and CO₂ emissions per km, BEV or PHEV electric range, traction (rear-, front- or 4-wheel), number of doors and seats, transmission, body style, and make (brand).

The upper nests of the model are defined as makes, while the lower level alternatives consist of the model variants offered within each make (Østli et al. 2017). Although the differences between certain car model variants are miniscule, they are all defined as separate units in the data set. There are 21 nests in the model, one for each of the 20 most common makes, plus a residual nest including ‘all other makes’. In total, the model contains 84 parameters. All 21 scale parameters characterizing the lower nests come out larger than unity, as required for consistency with random utility maximization (Ben-Akiva and Lerman 1985).

The effect of electric range on utility cannot be assumed to be linear. To investigate this, the electric ranges of BEVs and PHEVs were specified, in our generic nested logit model, as flexible form Box-Cox functions (Box and Cox 1964; Gaudry and Wills 1978):

$$x^{(\lambda)} = \begin{cases} \frac{x^{\lambda} - 1}{\lambda} &\text{if}\ \lambda \neq 0\ (x > 0)\\ \ln(x) &\text{if}\ \lambda = 0(x > 0) \end{cases}$$

The Box-Cox parameter λ determines the curvature of the relationship. λ = 2 corresponds to a quadratic function, λ = 1 to a linear one, λ = 0.5 to a square root, λ = 0 to a logarithmic function, and λ = –1 to a reciprocal one. The Box-Cox function is continuous even for λ = 0, since

$$\lim_{\lambda \rightarrow 0}\left( \frac{x^{\lambda} - 1}{\lambda} \right) = \ \ln(x).$$

Let U_i denote the partial utility of all-electric range, let p denote the vehicle’s price, and let r_i denote the all-electric range of cars with powertrain i. Then we can write

$$\begin{align} U_{i} &= \alpha_{p}p + \ \alpha_{i} r_{i}^{\left( \lambda_{i} \right)} \left( i = 1\ \text{for}\ BEVs,\ 2\ \text{for} PHEVs \right) \\ &= \ \left\{ \begin{matrix} \alpha_{p}p + \ \alpha_{i}(r_{i}^{\lambda_{i}} - 1)/\lambda_{i} & \text{if}\ \lambda_{i}\ \neq 0 \\\alpha_{p}p + \ \alpha_{i}\ln(r_{i}) & \text{if}\ \lambda_{i} = 0 \\ \end{matrix} \right. \end{align} \tag{1}$$

where α_p < 0 and α_i > 0 are slope coefficients, while λ₁ and λ₂ are Box-Cox (curvature) parameters.

The marginal willingness-to-pay for extended electric range can be computed as

$$- \frac{\frac{\partial U_{i}}{\partial r_{i}}}{\frac{\partial U_{i}}{\partial p}} = \ - \frac{\alpha_{i}}{\alpha_{p}}r_{i}^{\lambda_{i} - 1}. \tag{2}$$

The willingness-to-pay for larger improvements in range – from, say, s₀ to s₁ – can be computed as the integral under the curve (2):

$$\begin {align}W_{0}^{1}\ &= - \int_{s_{0}}^{s_{1}}{\frac{\alpha_{i}}{\alpha_{p}}r_{i}^{\lambda_{i} - 1}}dr_{i} \\&= - \frac{\alpha_{i}}{{\lambda_{i}\alpha}_{\text{p\ }}}\left\lbrack s_{1}^{\lambda_{i}} - s_{0}^{\lambda_{i}} \right\rbrack (i = BEV,PHEV)\end{align}\tag{3}$$

3. Findings

Selected results from the maximum likelihood estimation of our generic nested logit model are shown in Table 1.

To find the best-fit pair of Box-Cox parameters for BEVs and PHEVs, a grid search was performed, resulting in Box-Cox parameters of λ₁ = –0.5 for BEVs and λ₂ = +0.3 for PHEVs.

With this specification, the price coefficient comes out at α_p = –0.189 and the range coefficients at α₁ = 13.3 and α₂ = 0.0433 (Table 1).

The ensuing empirical Box-Cox partial utility functions (cf. equation 1) are depicted in Figure 1. The utility of a BEV or PHEV is a concave function of its (all-)electric range. Concavity is more pronounced for BEVs than for PHEVs.

Figure 1.Estimated relationship between partial utility and all-electric range of BEVs or PHEVs.

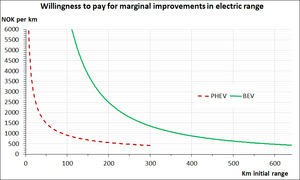
The marginal willingness-to-pay for extended range (2) is plotted in Figure 2. At 150 km initial BEV range, the value of an extra kilometer BEV range comes out at NOK 3792 = ca. € 354 as converted at the July 1, 2020 exchange rate (€ 1 = NOK 10.70). At 500 km initial BEV range, the value drops to NOK 629 = ca. € 59 per km.

For PHEVs, the marginal willingness-to-pay is much lower than for BEVs, coming out at NOK 1482 = ca. € 139 per km at 50 km initial all-electric range, and at NOK 912 = ca. € 85 at 100 km initial range.

Figure 2.Estimated willingness-to-pay for marginal improvements in the all-electric range of BEVs or PHEVs.

In Figure 3, we exhibit the willingness-to-pay for 100 km extended range (3). At 150 km initial BEV range, the value is NOK 259 000 = ca. € 24 200. At 500 km initial BEV range, the value of a 100 km further extension has dropped to NOK 55 000 = ca. € 5140.

Figure 3.Estimated willingness-to-pay for 100 km extended all-electric range in BEVs or PHEVs.

Can these results be generalized to other countries or jurisdictions? We think yes, with some reservations.

Norway’s record fast market uptake of battery and plug-in hybrid electric cars (75 percent in 2020) has given rise to an abundance of automobile transactions data fairly well balanced between the main five powertrain technologies. In our empirical discrete choice model, we are able to control for a large number of vehicle attributes – including size, make, body style, list price, and energy costs – in order to distil the partial effect of electric range per se.

But we have not been able to take into account contextual factors that might be systematically different between Norway and other countries. Fridstrøm (2021) lists the following reasons why battery electric cars may be more competitive in Norway than elsewhere: cheap and abundant electricity, strong power grids, widespread (semi-)detached housing with garage or driveway, ample roadside space for fast charging facilities, slow roads, strong governance, high income, and pervasive tolling, from which zero emission vehicles might conceivably be exempted.

Acknowledgements

This research was funded by the Research Council of Norway (grant 280989 ‘Integrated Transport and Energy Modelling’, grant 267942 ‘Driving Towards the Low-Emission Society’, and grant 295789 ‘PLATON – a Platform for Open and Nationally Accessible Climate Policy’).