Distributions of Bus Stop Spacings in the United States

1. Questions

Bus stop spacing refers to the distance that a bus travels from one stop to the next. Much theoretical analysis has focused on the choice of bus stop spacing (see extensive discussions in Daganzo and Ouyang 2019), which impacts how much time is spent braking and accelerating at stops as well as walking distances. Still, there is little hard data available as to what stop spacings actually are in the United States. One refrain in the literature is that US cities commonly have seven to ten bus stops per mile (Furth and Rahbee 2000; El-Geneidy et al. 2006). The source for this claim can be traced to Reilly (1997, 4), who says “It is common European practice to have stops spaced at 3 or 4 per mile in contrast with 7 to 10 stops per mile, which is common in the United States,” though the study does not cite a particular source for this fact.

This study uses General Transit Feed Specification (GTFS) (Wong 2013) data published by 43 US transit agencies to build a dataset of stop spacings, available at Pandey and Lehe (2021a), in which each row represents one traversal of a spacing. By “traversal” we mean one instance of a bus traveling from one stop to the next stop on the trip. The GTFS files were all published in late 2019—before the service changes wrought by COVID-19. This article introduces the dataset, defines terms and answers some questions using the database:

1. What are the summary statistics?

2. How do the distributions of stop spacings look?

3. How do mean stop spacings differ inside and outside of the “core” cities served by an agency?

2. Methods

2.1. Definitions

We define stop spacing as the distance between two stops along the route of the bus. It includes the distance traveled along any bends in the road.

For distributions and summary statistics of stop spacings, we apply what we call traversal weighting: that is, if the schedule has buses move directly from stop A to stop B 100 times before the schedule repeats, then that spacing is counted 100 times.

To illustrate, consider the simple bus system shown in Figure 1, which shows a network with two routes and three stops. The blue route has two stops spaced 400 m apart and a frequency of 1. The red route has three stops, spaced 200 m apart, and a frequency of 3. The traversal-weighted mean stop spacing for the network in Figure 1 is

$$\frac{400 + 200\cdot3 + 200\cdot3}{1 + 3\cdot2} = 228.57 \quad \textit{(m)}. \tag{1}$$

If an omnipresent driver were to drive every bus, this is the mean distance he or she would travel between stops on this network.

Figure 1.Example Transit Network

2.2. Calculation

Pereira, Andrade, and Bazzo (2020) introduces an R-package, gtfs2gps, which converts GTFS files to a database in which each row describes the location of a vehicle on a scheduled trip at a point along its route—including at all stops. One piece of data in each row is the cumulative distance that the vehicle has traveled since the start of the current trip. We use this database to produce another database, akin to the one in Table 1, in which each row represents one traversal, giving the distance traveled between the traversal’s two stops and their locations. Example code doing so for Ann Arbor is at Pandey and Lehe (2021b).

The general procedure is as follows: First, starting with the initial database produced by gtfs2gps, we filter out all non-bus trips and all rows that do not correspond to a location at a stop, so that the database only contains information about buses when they are at stops. Next, for each stop along each trip, we subtract the cumulative distance traveled (from the start of the trip) when the bus is at the preceding stop from the cumulative distance traveled at the given stop, which gives the distance traveled between the stops. This difference is stored as a row in the new database along with both stops’ coordinates, and the database is made available at Pandey and Lehe (2021a).

3. Findings

We apply the method described in Sec. 2.2 to 43 US cities. The sample includes the six most populated US cities as well as many smaller cities chosen to capture a diversity of city types and regions. The only systematic requirement for inclusion was that a city’s GTFS files be sufficiently “filled in” for gtfs2gps to convert the GTFS files to a GPS database. To run gtfs2gps requires that a GTFS bundle includes certain files: the optional ‘shapes.txt’ file and either the optional ‘frequency.txt’ or certain optional columns in the required ‘stop_times.txt’ file, so it cannot run when agencies do not include some optional data. The particular agency corresponding to each city^[1] is listed in Table 2.

The database can be put to several uses. One is to compare summary statistics. (To aid comparison, Table 3 translates into meters the 3, 7, 4 and 10 stops per mile mentioned in Reilly 1997.) Summary statistics appear in Table 2, where Q25 and Q75 refer to the 25^thand 75^thpercentile, respectively. The Southeastern Pennsylvania Transportation Authority in Philadelphia has the narrowest mean stop spacing of 223 m, while Las Vegas’ Regional Transportation Commission of Southern Nevada the widest at 446 m. The mean spacing across the whole dataset is 313 m, which amounts to slightly more than 5 stops per mile.

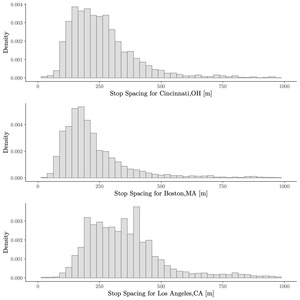
Alternatively, we can also visualize distributions of spacings. Figure 2 shows histograms of the stop spacing distributions for Cincinnati, Boston, and Los Angeles. Note that Boston’s spacings are distributed more tightly than those of Los Angeles.

Figure 2.Traversal-weighted stop spacing distributions

The database can also be combined with geographic data, since we include the locations of both stops in each spacing. As a simple illustration, we use city boundary shapefiles downloaded from Centers for Disease Control and Prevention (2020) to calculate the mean spacing inside and outside each agency’s “core” city, which we define to be the most populated city that the agency serves. If both stops involved in a traversal fall within the core city, we classify the traversal as being inside the core. The last two columns of Table 2 list the resulting means, and Figure 3 visualizes them. Note several facts. First, spacings are generally larger than 7 per mile, and in some cities within the band of 3 to 4 stops per mile claimed to be typical of European cities. Second, stop spacings are larger outside than inside core cities. Third, cities mostly established before the automobile era (e.g., Cleveland) have relatively smaller spacings.

Figure 3.Average Stop Spacing inside and outside core city

This exercise also demonstrates why it is critical for comparisons to be clear about sourcing. For instance, Chicago’s suburban communities are mainly served by PACE Suburban Bus, but our dataset for Chicago comes from the Chicago-focused CTA; hence, the spacing inside and outside the core are similar.

The authors hope the dataset and code provided can serve many purposes. US agencies have tried to consolidate bus stops—e.g., Pittsburgh most recently (Blazina 2020)—and decision-makers might benefit from knowing how their cities’ spacings compare. Similar data could also be collected for cities in other countries. Spacings may also be classified by census tract to answer questions such as: does stop spacing decline with population and/or job density? It may also be worthwhile for researchers to write code targeted more efficiently at studying stop spacings than gtfs2gps is.