The analysis of travel demand often includes the partitioning of the demand into “market segments” seeking to separate these influences into groups. As demonstrated in (Travel Demand Modelling 2016; Ben-Akiva and Lerman 1987; Limtanakool, Dijst, and Schwanen 2006; Bhat 1997b; Koppelman and Sethi 2000; Mandel, Gaudry, and Rothengatter 1997; Larse 2010; Wardman, Toner, and Whelan 1997; LaMondia, Bhat, and Hensher 2008; Carlsson 1999; Hensher 1991; Morrison and Winston 1985; Hassanvand 2020), the development of such models includes substantial effort that encompasses enormous revalidation work, which has been reduced with the aid of advanced computer technology. However, there still exists a gap in model design that arise from failure to segment markets.

This paper defines travel alternatives made by market segments with the aim of optimizing the selection of descriptive variables and strengthening the explanatory power of the model. Nearly all long-distance person trips (LDPT) models (Federal Highway Administration 2015; Golob 2001; Kizielewicz et al. 2017; Bhat 1997a; Golob and Hensher 1998; Badoe and Miller 1998; Lieberman et al. 2001) developed in various countries are based not on empirical procedures but rather by educated guesses to describe the travel market variables. This research transforms the approach to traditional segmentations using computer science approaches for network-based data that stem from fuzzy logic (Zadeh 1965). Such approaches are based on grouping of data points by examining their proximity (e.g. Euclidean distance) to one another. This is essential as LDPT is not merely the longer version of short-distance daily trips. While fuzzy-neuro models have been used in transit and some short-distance models (Kumar, Sarkar, and Madhu 2013; Sarkar 2012; Tharwat 2014; Roxas 2016; Yaldi et al, n.d.; Gite 2013), they have not been used in LDPT – excluding goods movement, trucking, or air travel.

METHODS AND DATA

Clustering is a statistical tool used in pattern recognition and machine learning to find similar groups in seemingly dissimilar network-based datasets (e.g. transport data). Objects in a cluster/class share many characteristics but are very dissimilar to objects not belonging to that particular cluster (Punj and Stewart 1983). In most of the classification works (Milligan 1996; Posse 1998; Everitt, Landau, and Leese 2001), considerable number of algorithms belong to two major types of clustering used here namely Hierarchical and Partitional. The former is based on finding clusters hierarchy using a criterion and producing a dendrogram. The latter is partitioning the data based on minimization of an objective function such as the squared error function (Kaufman and Rousseeuw 1990; Bezdek 1974):

J=∑kj=1 ∑ni=1‖x(j)i−cj‖2(1)

Where ‖x(j)i−cj‖2 is the distance between a data item x(j)i and a centre point cj.

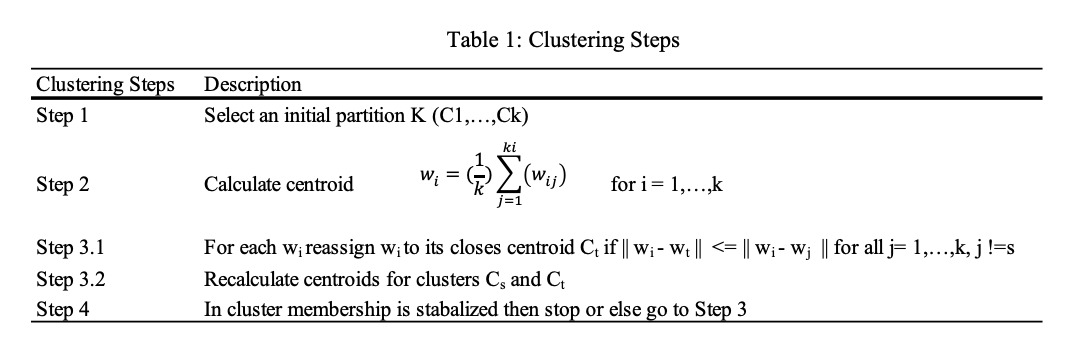
One type of partitional clustering, with steps shown in Table 1, is called the k-means approach as a specific form of the more general fuzzy c-means clustering that minimizes a similar objective function [34]:

Table 1
Table 1:Clustering Steps

The uniqueness of this work lies partly in the essential three-step cluster validity checks which are often ignored in many clustering themed studies (Dunn 1974; Zaki and Meira, Jr 2014):

  1. Cluster tendency checks: which is a measure of clusterability of a data set considering that algorithms such as k-mean unquestioningly find some clusters in a data set regardless. Thus, to ensure the data is actually clusterable, one must examine it for its clustering tendency using indices such as the Hopkins statistics prior to any clustering practices.

  2. Cluster stability checks: is the practice of clustering randomly generated data sets out of the original data and data belonging to other years/locations in order to examine if the resulting clusters are persistent and show up each time. Also, clustering the data set using fuzzy c-means provides an additional check on the existence/lack of potential outliers and acts as a precautionary measure against model-dependency of results.

  3. Cluster validity: consists of three tests namely External (one-way ANOVA, Post-hoc Bonferroni, and Logistic Regression), Internal (Beta-CV index), and Relative (Elbow method). Other tests include variables’ correlation checks, F-tests, Grubb’s test of outliers, Ward’s (AHC) dendrogram analyses and stopping rules comparison of a large Duda-Hart Je(2)/Je(1) index with a small Pseudo T-tests and a large Calinski-Harabasz Pseudo-F indices for detection of number of clusters (Everitt, Landau, and Leese 2001).

The publicly available standardized and weighted 2017 Travel Survey of Residents of Canada (TSRC) data set – including 14064 Province of Alberta (AB) residents, 4167 AB to AB trips, and 6128 nights travelled – is examined and compared with 2016 and 2015 data. TSRC is a supplement of the Canadian Labour Force Survey (LFS) (Statistics Canada 2017b, 2017a) after which TSRC questions are asked of a random 18+ household (HH) member regarding any one-way 40+ km trips from home finished in the previous month (same-day/overnight) plus any overnight trips ended two months before regardless of distance. Figure 1 shows trip counts by distance/purpose followed by variables’ list in Table 2. Analysis is based on 100 variables with minimal correlations from socio-demographic factors to places visited and 37 different activities divided into same-day/overnight.

Figure 1
Figure 1:Count of Trips by Distance and Canadian Nights Away for 2017 (TSRC) 4167 (AB) to (AB) Trips
Table 2
Table 2:List of Variables

FINDINGS

Table 3 describes 10 clusters found in the 2017 data set followed by Figure 2 which is a 3D representation of clusters’ center points across some of the most important dimensions (for brevity). Figure 3 represents a dendrogram of classes hierarchy found through (AHC) clustering.

Table 3
Table 3:Clusters Found in the 2017 (TSRC) (AB) to (AB) Trips at 68% Confidence Level
Figure 2
Figure 2:3D Representation of 10 Clusters Across a few Key Dimensions: Household (HH) Members on the Trip, Travelling Group Size, Total Nights Away from home while on Trip, One-way Distance from Home in km, Trips Frequency, Total Amount of Spending while on Trip in 2017 $CAD
Figure 3
Figure 3:2017 (TSRC) (AB) to (AB) Trips (AHC) Ward’s Dendrogram

Examinations revealed the data possess a natural structure with 10 clusters at 68% confidence level. Such results are consistent with other literature findings for LD trips (Future Foundation 2015; Birley and Westhead 1990; Mooi and Sarstedt 2011). For example, trips done for pleasure have consistently been found to belong to mostly the top two categories of LDPT. The second largest cluster is representative of individual adults from the same HH who travel in smaller groups with no kids. Their purpose is mainly same-day trips of shopping with moderate levels of spending with activities such as walking. This finding is novel and could be a characteristic of the Province of Alberta, in that malls and shopping centres such as Banff, Lake Louise, West Edmonton mall, or other shopping avenues are also long-distance traveller attractors. The existence of such clusters demonstrates how traditional LDPT trips segmentation through “guessing variables and rechecking” are obsolete and would need to be enhanced using comprehensive clustering approaches targeted for network-based data to better represent the overall LDPT market while relying less on conjecture and assumptions.